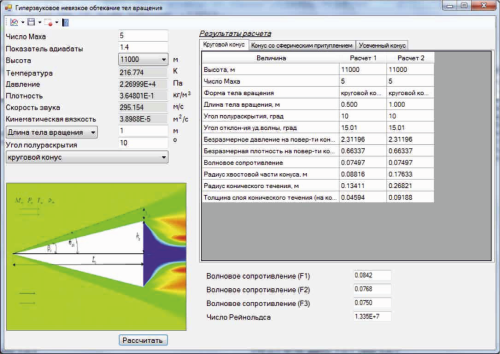
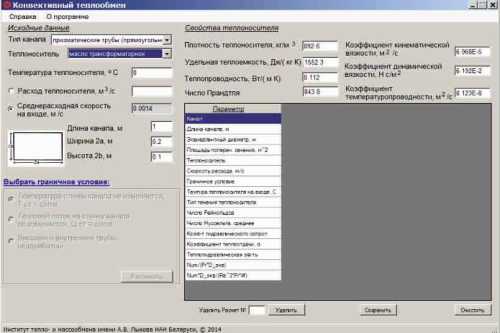
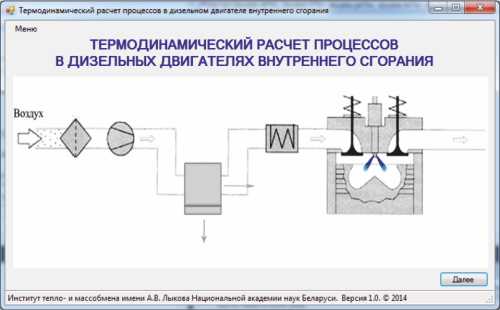
Свидетельство № 1715-КП о регистрации компьютерной программы «Термогидродинамический режим работы теплообменника проточного типа». Год создания: 2023. Авторы: Войцеховская Н.Г., Сидорович Т.В., Чорный А.Д. Дата подачи заявки (регистрации и депонирования): 27.03.2024.
Тиунов С.В., Скрыпник А.Н., Маршалова Г.С., Гуреев В.М., Попов И.А., Кадыров Р.Г., Чорный А.Д., Жукова Ю.В. Экспериментальное исследование теплогидравлических характеристик оребренных плоских труб аппарата воздушного охлаждения масла// Энергетика.Известия высших учебных заведений и энергетических объединений СНГ - 2020
С.А. Исаев, А.Д. Чорный, Ю.В. Жукова, Фролов Д.П., Юнаков Л.П. Согласованные граничные условия на входе в расчетную область на примере моделирования ламинарного обтекания пластинки.// ИФЖ -2020
А.Д. Чорный, Т.А. Баранова, Ю.В. Жукова, С.А. Исаев. Использование упорядоченной шероховатости для интенсификации теплообмена в микроканалах при течении в них гелия//Вестник Фонда фундаментальных исследований-2020
М.В. Гуреев, И.И. Хабибуллин, А.Н. Скрыпник, Г.С. Маршалова, И.А. Попов, Р.Г. Кадыров, В.М. Гуреев, А.Д. Чорный, Ю.В. Жукова. Определение рациональных компоновочных решений аппарата воздушного охлаждения масла систем смазки компрессорных установок с использованием методов физического и численного моделирования.// Вести Национальной академии наук Беларуси. Физико-техническая серия -2020
Т.А. Баранова, Ю.В. Жукова, А.Д. Чорный. Турбулентное смешение неизотермических потоков в канале тройникового соединения//Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси-2020
А.N. Skrypnik, А.М. Еrmakov, R.T. Каlimullin, А.А. Mironov, I.А. Popov, А.D. Chorny, Yu.V. Zhukova, G.S. Experimental and numerical study of the characteristics of fin-tube oil radiators of power engineering devices//Heat Transfer Research-2020
М.В. Гуреев, А.М. Ермаков, Ю.В. Жукова, Р.Г. Кадыров, Р.Р. Калимуллин, Г.С. Маршалова, А.А. Миронов, Р.М. Низамутдинов, И.А. Попов, А.Н. Скрыпник, С.В. Тиунов, Р.А. Усенков, И.И. Хабибуллин, А.Д. Чорный. Повышение надежности прогнозирования теплогидравлических характеристик трубчато-ребристых радиаторов аппаратов воздушного охлаждения энергоустановок на основе численного и экспериментального исследования//Тепловые процессы в технике - 2020
А.В. Баранюк, В.А. Рогачев, Ю.В. Жукова, А.М. Терех, А.И. Руденко. Экспериментальное исследование теплообмена плоских теплоотводящих поверхностей с пластинчатым оребрением//Экспериментальное исследование теплообмена плоских теплоотводящих поверхностей с пластинчатым оребрением -2020
Yu.V. Zhukova, А.М. Terekh, S.А. Isaev, E.N. Pis’menny. Aerodynamic characteristics and heat transfer of a single oval-shaped cylinder at different Reynolds numbers//Heat Transfer Research
V. Rohachev, A. Terekh, A. Baranyuk, Yu. Nikolaenko, Yu. Zhukova, A. Rudenko. Heataerodynamic efficiency of small size heat transfer surfaces for cooling thermally loaded electronic components//Thermal Science and Engineering Progress - 2020
Д. И. Кривовязенко, А.Д.Чорный, Е.М.Заяц. Электрическая коагуляция белков молочной сыворотки//Агропанорама -2020
Кот В. А. Новый подход в приближенном решении задачи Стефана с конвективным граничным условием//Доклады НАН РБ - 2020
Кот В. А. Комбинированный метод разделения переменных. 1. Метод координатных функций: критический анализ//ИФЖ
Кот В. А. Комбинированный метод разделения переменных. 2. Последовательности дифференциальных соотношений: пластина, цилиндр, шар//ИФЖ
Кот В. А. Новые представления в приближенном математическом описании однофазной задачи Стефана с конвективным граничным условием на фиксированной границе: решение// Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси -2020
Кот В. А. Новые представления в приближенном математическом описании однофазной задачи Стефана с конвективным граничным условием на фиксированной границе: анализ //Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси-2020
Механика жидкости и газа. Методическое пособие / В.Г.Баштовой, А.Г.Рекс, А.Д.Чорный. Минск: БНТУ, 2012. 56 с.
Babenko V.A., Frost V.A. Approximation accuracy of the two-point third moments of the velocity field in the homogeneous turbulence, International Journal of Heat and Mass Transfer, Volume 55, Issue 9-10, April 2012, Pages 2676-2683. (импакт-фактор 2.657)
В.А. Кондратюк, В.Е. Туз, А.М. Терех, Ю.В. Жукова, А.Ж. Мейрис, Аэродинамическое сопротивление поперечно-омываемых шахматных пакетов плоскоовальных труб, Восточно-Европейский журнал передовых технологий, 3/8 (57), стр. 39–42, 2012.
Chorny A., Zhdanov V. Turbulent mixing and fast chemical reaction in the confined jet flow at large Schmidt number // Chem. Eng.Sci. 2012. Vol. 68. Pp. 541–554. (импакт-фактор 1.828)
Ю.В. Жукова, А.В. Киреенко, Интенсификация теплообмена при течении теплоносителя в круглой трубе с продольным внутренним оребрением, Тез. 10 Международной научно-практической конференции аспирантов, магистрантов, студентов «Современные проблемы научного обеспечения энергетики», Киев, 17-20 апреля 2012, с. 223.
С.А. Исаев, А.И. Леонтьев, М.Е. Гульцова, С.В. Гувернюк, М.А. Зубин, А.Ю. Чулюнин, Н.В. Корнев, В.Л. Жданов, Ю.В. Жукова, В.В. Воскобойник, В. Тимченко, Интенсификация тепломассообменных процессов в микро- и макроканалах – трубах в неоднородных средах поверхностными вихрегенераторами – лунками, Материалы 12 Международной школы-семинара «Модели и методы аэродинамики», Евпатория, 4-13 июня 2012, М.: МЦНМО, 2012. с.106-108.
А.Г. Судаков, С.А. Исаев, П.А. Баранов, О.А. Бояркина, С.В. Гувернюк, М.А. Зубин, А.А. Чулюнин, А.А. Синявин, А.Е. Усачов, Ю.В. Жукова, В.Т. Гринченко, Г.А. Воропаев, Н.В. Розумнюк, В.В. Воскобойник, Управление обтеканием тел (профили и крылья, лопатки турбин, оребренные трубы) с помощью вихревых ячеек, поверхностных и объемных вихрегенераторов, Материалы 12 Международной школы-семинара «Модели и методы аэродинамики», Евпатория, 4-13 июня 2012, М.: МЦНМО, 2012. с.184-185.
Ю. В. Жукова, Численное исследование аэродинамических характеристик и теплоотдачи поперечно-обтекаемых пакетов труб круглого сечения с внешними интенсификаторами, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 94-96.
Ю. В. Жукова, А. Д. Чорный, Интенсификация теплообмена при течении теплоносителя в трубах с внутренним продольным оребрением, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 97-99.
С. А. Исаев, П. А. Баранов, С. В. Гувернюк, О. О. Егорычев, О. И. Поддаева, Ю. В. Жукова, А. Д. Чорный, А. Е. Усачов, Б. И. Басок, Н. В. Корнев, Энергоэффективные высотные сооружения на основе использования принципа управления крупномасштабными вихревыми структурами и ветроэнергетических установок, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 109-111.
А. В. Киреенко, Ю. В. Жукова, Использование пакета OpenFoam для расчета сопряженных задач конвективного теплообмена, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 135-136.
Дударева И. Г., Чорный А. Д. моделирование аэродинамики планера в виртуальной аэродинамической трубе // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 84-86.
Кухарчук И. Г., Чорный А. Д. экспериментальное исследование гидродинами-ческой кавитации в проточных каналах смесителей // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 160-161.
Чорный А. Д., Заяц Е. М., Кривовязенко Д. И. расчет параметров теплопереноса при электрокоагуляции белков молочной сыворотки // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 345-348.
Шахновская А. А., Чорный А. Д. расчет теплообмена в системах остекления с интегрированными нагревателями // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 357-358.
Фрост В. А., Бабенко В.А. перемешивание в однородной турбулентности // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 326-329.
Бабенко В.А., Баранова Т. А., Гнездилов Н. Н., Козлов И. М., сметанников А. С. моделирование высокоскоростного удара методом сглаженных частиц // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 326-329.
Список публикаций 2006-20011. Скачать.
С.А. Исаев, А.Д. Чорный, Ю.В. Жукова, Фролов Д.П., Юнаков Л.П. Согласованные граничные условия на входе в расчетную область на примере моделирования ламинарного обтекания пластинки.// ИФЖ -2020
А.Д. Чорный, Т.А. Баранова, Ю.В. Жукова, С.А. Исаев. Использование упорядоченной шероховатости для интенсификации теплообмена в микроканалах при течении в них гелия//Вестник Фонда фундаментальных исследований-2020
М.В. Гуреев, И.И. Хабибуллин, А.Н. Скрыпник, Г.С. Маршалова, И.А. Попов, Р.Г. Кадыров, В.М. Гуреев, А.Д. Чорный, Ю.В. Жукова. Определение рациональных компоновочных решений аппарата воздушного охлаждения масла систем смазки компрессорных установок с использованием методов физического и численного моделирования.// Вести Национальной академии наук Беларуси. Физико-техническая серия -2020
Т.А. Баранова, Ю.В. Жукова, А.Д. Чорный. Турбулентное смешение неизотермических потоков в канале тройникового соединения//Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси-2020
А.N. Skrypnik, А.М. Еrmakov, R.T. Каlimullin, А.А. Mironov, I.А. Popov, А.D. Chorny, Yu.V. Zhukova, G.S. Experimental and numerical study of the characteristics of fin-tube oil radiators of power engineering devices//Heat Transfer Research-2020
М.В. Гуреев, А.М. Ермаков, Ю.В. Жукова, Р.Г. Кадыров, Р.Р. Калимуллин, Г.С. Маршалова, А.А. Миронов, Р.М. Низамутдинов, И.А. Попов, А.Н. Скрыпник, С.В. Тиунов, Р.А. Усенков, И.И. Хабибуллин, А.Д. Чорный. Повышение надежности прогнозирования теплогидравлических характеристик трубчато-ребристых радиаторов аппаратов воздушного охлаждения энергоустановок на основе численного и экспериментального исследования//Тепловые процессы в технике - 2020
А.В. Баранюк, В.А. Рогачев, Ю.В. Жукова, А.М. Терех, А.И. Руденко. Экспериментальное исследование теплообмена плоских теплоотводящих поверхностей с пластинчатым оребрением//Экспериментальное исследование теплообмена плоских теплоотводящих поверхностей с пластинчатым оребрением -2020
Yu.V. Zhukova, А.М. Terekh, S.А. Isaev, E.N. Pis’menny. Aerodynamic characteristics and heat transfer of a single oval-shaped cylinder at different Reynolds numbers//Heat Transfer Research
V. Rohachev, A. Terekh, A. Baranyuk, Yu. Nikolaenko, Yu. Zhukova, A. Rudenko. Heataerodynamic efficiency of small size heat transfer surfaces for cooling thermally loaded electronic components//Thermal Science and Engineering Progress - 2020
Д. И. Кривовязенко, А.Д.Чорный, Е.М.Заяц. Электрическая коагуляция белков молочной сыворотки//Агропанорама -2020
Кот В. А. Новый подход в приближенном решении задачи Стефана с конвективным граничным условием//Доклады НАН РБ - 2020
Кот В. А. Комбинированный метод разделения переменных. 1. Метод координатных функций: критический анализ//ИФЖ
Кот В. А. Комбинированный метод разделения переменных. 2. Последовательности дифференциальных соотношений: пластина, цилиндр, шар//ИФЖ
Кот В. А. Новые представления в приближенном математическом описании однофазной задачи Стефана с конвективным граничным условием на фиксированной границе: решение// Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси -2020
Кот В. А. Новые представления в приближенном математическом описании однофазной задачи Стефана с конвективным граничным условием на фиксированной границе: анализ //Тепло- и массоперенос – 2019: сб. науч. тр. Минск: Институт тепло- и массопереноса им. А. В. Лыкова НАН Беларуси-2020
| Название | Издательство, журнал | Авторы | |
|---|---|---|---|
| 1. | Теплофизика. Термодинамика и статистическая физика | Учебное пособие. – Минск: Вышэйшая школа, 2018. – 447 с. | В. И. Байков, Н.В. Павлюкевич |
| 2 | Теплофизика. Неравновесные процессы тепломассопереноса | учебное пособие. – Минск: Вышэйшая школа, 2018. – 476 с. | В. И. Байков, Н.В. Павлюкевич, А.К.Федотов, А.И. Шнип |
| 3. | Влияние структуры предотрывного течения на характеристики зоны отрыва за обратным уступом. | ИФЖ, Т.91, N3, pp. 628- 640, 2018. | В.Л. Жданов, Д. Иванов, Я.И.Смульский, В.И. Терехов |
| 4. | Численный анализ присоединенного течения за ребром. | Доклады академии наук Беларуси. Т. 61, №3, 2018. | Т.А. Баранова, В.Л. Жданов, Д. А. Иванов, Я.И.Смульский, В.И. Терехов. |
| 5. | Terekhov V.I. RANS and LES analysis of a separation region in front of a backward-facing step | Journal of Physics: Conf. Series 980 (2018) 012026; doi :10.1088/1742-6596/980/1/012026. | Baranova T.A., Zhdanov V. L. Ivanov D.A., Smulski Ja. I., Terekhov |
| 6. | Теплогидравлическая эффективность труб с внутренним спиральным оребрением | ИФЖ, т.91, № 1, с. 58–69, 2018 | А.Н. Скрыпник, А.В. Щелчков, И.А. Попов, Д.В. Рыжков, С.А. Сверчков, Ю.В. Жукова, А.Д. Чорный, Н.Н. Зубков |
| 7. | Вихревая интенсификация теплообмена при ламинарном обтекании кругового и эллиптического цилиндров воздухом и маслом | ИФЖ, т.91, № 3, с. 664–672, 2018. | С.А. Исаев, Ю.В. Жукова, И.А. Попов, А.Г. Судаков, |
| 8. | Верификация физико-математической модели для расчета аэродинамических характеристик плохообтекаемых тел, движущихся в воздухе при больших числах Маха | Системный анализ и прикладная информатика, № 3, стр. 42–47, 2018 | А.Д. Чорный, А.Н. Чичко, Ю.В. Жукова, И.Г. Кухарчук, А.Ф. Мелец, В.А. Малкин |
| 9. | Convective heat transfer and drag of two side-by-side tubes in the narrow channel at different Reynolds number | Doklady of the National Academy of Sciences of Belarus, 2018, Vol. 62, No 6. | Yu. V. Zhukova, A. М. Теrekh, A.I. Rudenko |
| 10. | A new look at the integral methods for solving heat and mass transfer | Journal of Physics: Conf. Series 1128 (2018) 012030. doi:10.1088/1742-6596/1128/1/052010. pp. 1–6. | Кот V.A. |
| 11. | Интегральные методы решения задач тепломассопереноса: новая концепция (условие Дирихле) | Доклады Национальной Академии Беларуси. 2018. Т. 62, № 6. | Кот В.А. |
| 12. | Интегральный метод граничных характеристик: условие Неймана | Инженерно-физический журнал. 2018. Т. 91, № 2. С. 469–496. | Кот В.А. |
| 13. | Обобщенное решение смешанной задачи теплопроводности методом взвешенной температуры | Инженерно-физический журнал. 2018. Т. 91, № 4. С. 1066–1088. | Кот В.А. |
| 14. | Параболический профиль в задачах теплопроводности. 1. Полуограниченное пространство с поверхностью постоянной температуры | Инженерно-физический журнал. 2018. Т. 91, № 6. С. 1463–1484. | Кот В.А. |
| 15. | Интегральный метод решения задач теплопроводности с граничным условием второго рода. 1. Основные положения | Известия Национальной академии наук Беларуси. Сер. физ.-техн. наук. 2018, T. 63. № 2. С. 201–213. | Кот В.А. |
| 16. | Интегральный метод решения задач теплопроводности с граничным условием второго рода. 2. Анализ точности | Известия Национальной академии наук Беларуси. Сер. физ.-техн. наук. 2018, T. 63. № 3. С. 318–332. | Кот В.А. |
| 17. | Методы снижения поверхностного трения турбулентного пограничного слоя. | В сб. Тепло- и массоперенос-2017: сборник научных трудов. Минск: ИТМО имени А.В. Лыкова НАН Беларуси, 2018. 9 с. | Жданов В.Л., Кухарчук И.Г. |
| 18 | Расчет динамики роста графена на медном катализаторе в процессах химического парофазного осаждения | В сб. Тепло- и массоперенос-2017: сборник научных трудов. Минск: ИТМО имени А.В. Лыкова НАН Беларуси, 2018. С.139-145 | Футько С. И., Чорный А.Д., Ермолаева Е. М. |
| 19 | Полиномиальное решение задачи Стефана для микро- и наноразмерной сферической частицы: условие Дирихле | Тепло- и массоперенос-2017. Минск: Институт тепло- и массообмена имени А.В. Лыкова НАН Беларуси, 2018. С. 234–250. | Кот В.А. |
| 20 | Аналитическое решение задачи Стефана о плавлении микро- и наноразмерной сферической частицы в условиях постоянного и гармонического теплового воздействия | Тепло- и массоперенос-2017. Минск: Институт тепло- и массообмена имени А.В. Лыкова НАН Беларуси, 2018. С. 251–268. | Кот В.А. |
| 21 | Многоблочные вычислительные технологии применительно к расчету турбулентных отрывных и струйных течений сжимаемого вязкого газа со скачками уплотнения и ударными волнами в рамках модели переноса сдвиговых напряжений, в: «Физика ударных волн, горения, детонации, взрыва и неравновесных процессов. Том 2 | стр. 216-228. Минск: Институт тепло- и массообмена имени А.В. Лыкова НАН Беларуси, 2018. | под ред. В.А. Левина, Н.А. Фомина, В.Е. Фортова. С. А. Исаев, А. Г. Судаков, П. А. Баранов, Ю. В. Жукова, А. Е. Усачов, |
| 22 | Вычислительный эксперимент от кластерного термоядерного синтеза до ударов планетарного масштаба | В книге Физика ударных волн, горения, взрыва, детонации и неравновесных процессов. Ч.2. Под. ред. В.А. Левина, Н.А. Фомина, В.Е. Фортова. Минск: ИТМО НАН Беларуси, 2018, С. 259-308 | Мисюченко Н. И., Рудак Л. В., Тетерев А. В., Чорный А.Д. |
| 23 | Турбулентный пограничный слой. Методы управления сдвиговыми напряжениями. | Препринт ИТМО НАНБ №1, 2018, 33с. | Жданов В.Л. |
| 24 | Experimental investigation of heat transfer in the separation zone behind a back-facing step in the presence of tabs | Proceedings of the 16th International Heat Transfer Conference, IHTC-16. August 10-15, 2018, Beijing, China. | A.Yu. Dyachenko, Ya. J. Smulsky, V.I. Terekhov, V.L. Zhdanov |
| 25. | Применение методов численного моделирования для оптимизации многопараметрических процессов в промышленности: некоторые задачи гидрогазодинамики и теплообмена | 3-я международная научно-практическая конференция «Наука – инновационному развитию общества», г. Минск, 15 ноября 2018 г. | А. Д. Чорный. |
| 26. | Ю.В.Жукова | Использование пакетов прикладных программ для решения задач конвективного теплообмена (проблемный доклад). | Конференция «Современные методы научного обеспечения энергетики» (НТУУ имени И. Сикорского, г. Киев, Украина). |
| 27 | О новых интегральных методах получения параболических решений задач теплопроводности | Труды Седьмой Российской национальной конференции по теплообмену (22—26 октября 2018 г., Москва). Т. 3. — М.: Издательский дом МЭИ, 2018. – С. 240–243 с. | Кот В.А. |
| 28. | Новый взгляд на интегральные методы решения задач тепломассопереноса | Тез. докл. III Всероссийской науч. конф. «Теплофизика и физическая гидродинамика», РФ, г. Ялта, 10 – 16 сентября 2018 г. С. 72. | Кот В.А. |
| 29 | Влияние поперечного шага установки труб в пучках однорядных воздухоохлаждаемых теплообменников из ребристых труб при смешанно-конвективном теплообмене | Труды Седьмой Российской национальной конференции по теплообмену (22—26 октября 2018 г., Москва). Т. 3. — М.: Издательский дом МЭИ, 2018. | Маршалова (Сидорик) Г.С. |
Babenko V.A., Frost V.A. Approximation accuracy of the two-point third moments of the velocity field in the homogeneous turbulence, International Journal of Heat and Mass Transfer, Volume 55, Issue 9-10, April 2012, Pages 2676-2683. (импакт-фактор 2.657)
В.А. Кондратюк, В.Е. Туз, А.М. Терех, Ю.В. Жукова, А.Ж. Мейрис, Аэродинамическое сопротивление поперечно-омываемых шахматных пакетов плоскоовальных труб, Восточно-Европейский журнал передовых технологий, 3/8 (57), стр. 39–42, 2012.
Chorny A., Zhdanov V. Turbulent mixing and fast chemical reaction in the confined jet flow at large Schmidt number // Chem. Eng.Sci. 2012. Vol. 68. Pp. 541–554. (импакт-фактор 1.828)
Ю.В. Жукова, А.В. Киреенко, Интенсификация теплообмена при течении теплоносителя в круглой трубе с продольным внутренним оребрением, Тез. 10 Международной научно-практической конференции аспирантов, магистрантов, студентов «Современные проблемы научного обеспечения энергетики», Киев, 17-20 апреля 2012, с. 223.
С.А. Исаев, А.И. Леонтьев, М.Е. Гульцова, С.В. Гувернюк, М.А. Зубин, А.Ю. Чулюнин, Н.В. Корнев, В.Л. Жданов, Ю.В. Жукова, В.В. Воскобойник, В. Тимченко, Интенсификация тепломассообменных процессов в микро- и макроканалах – трубах в неоднородных средах поверхностными вихрегенераторами – лунками, Материалы 12 Международной школы-семинара «Модели и методы аэродинамики», Евпатория, 4-13 июня 2012, М.: МЦНМО, 2012. с.106-108.
А.Г. Судаков, С.А. Исаев, П.А. Баранов, О.А. Бояркина, С.В. Гувернюк, М.А. Зубин, А.А. Чулюнин, А.А. Синявин, А.Е. Усачов, Ю.В. Жукова, В.Т. Гринченко, Г.А. Воропаев, Н.В. Розумнюк, В.В. Воскобойник, Управление обтеканием тел (профили и крылья, лопатки турбин, оребренные трубы) с помощью вихревых ячеек, поверхностных и объемных вихрегенераторов, Материалы 12 Международной школы-семинара «Модели и методы аэродинамики», Евпатория, 4-13 июня 2012, М.: МЦНМО, 2012. с.184-185.
Ю. В. Жукова, Численное исследование аэродинамических характеристик и теплоотдачи поперечно-обтекаемых пакетов труб круглого сечения с внешними интенсификаторами, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 94-96.
Ю. В. Жукова, А. Д. Чорный, Интенсификация теплообмена при течении теплоносителя в трубах с внутренним продольным оребрением, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 97-99.
С. А. Исаев, П. А. Баранов, С. В. Гувернюк, О. О. Егорычев, О. И. Поддаева, Ю. В. Жукова, А. Д. Чорный, А. Е. Усачов, Б. И. Басок, Н. В. Корнев, Энергоэффективные высотные сооружения на основе использования принципа управления крупномасштабными вихревыми структурами и ветроэнергетических установок, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 109-111.
А. В. Киреенко, Ю. В. Жукова, Использование пакета OpenFoam для расчета сопряженных задач конвективного теплообмена, Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 135-136.
Дударева И. Г., Чорный А. Д. моделирование аэродинамики планера в виртуальной аэродинамической трубе // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 84-86.
Кухарчук И. Г., Чорный А. Д. экспериментальное исследование гидродинами-ческой кавитации в проточных каналах смесителей // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 160-161.
Чорный А. Д., Заяц Е. М., Кривовязенко Д. И. расчет параметров теплопереноса при электрокоагуляции белков молочной сыворотки // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 345-348.
Шахновская А. А., Чорный А. Д. расчет теплообмена в системах остекления с интегрированными нагревателями // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 357-358.
Фрост В. А., Бабенко В.А. перемешивание в однородной турбулентности // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 326-329.
Бабенко В.А., Баранова Т. А., Гнездилов Н. Н., Козлов И. М., сметанников А. С. моделирование высокоскоростного удара методом сглаженных частиц // Труды Минского международного форума по тепломассообмену ММФ–XIV, Минск, 10–13 сентября 2012 г., с. 326-329.
Список публикаций 2006-20011. Скачать.